代码随想录Day16

 · 2024-1-16 · 次阅读

二叉树 | 222. 完全二叉树的节点个数|

222 完全二叉树的节点个数

简单解法：层序遍历法： O(n) 后序递归法O(n);

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int countNodes(TreeNode* root) {
        queue <TreeNode *> que;
        int count=0;
        if(root!=NULL) que.push(root);
        while(!que.empty()){
            TreeNode* cur;
            int size =que.size();
            while(size--){
                cur=que.front();
                que.pop();
                count++;
                if(cur->left) que.push(cur->left);
                if(cur->right) que.push(cur->right);
            }
        }
        return count;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 后序递归法
class Solution {
public:
    int GetNodeNum(TreeNode * cur){
        if(cur==NULL) return 0;
        int LeftNum =GetNodeNum(cur->left);
        int RightNum =GetNodeNum(cur->right);
        int treeNum =LeftNum+RightNum+1;
        return treeNum;
    }

    int countNodes(TreeNode* root) {
        return GetNodeNum(root);
    }
};

思路： 基于完全二叉树的性质进行优化

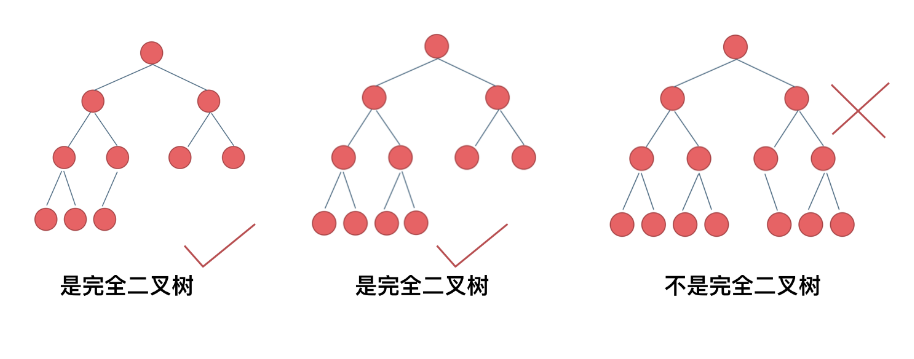
image-20240118001747262

不遍历完全二叉树的所有节点，

在满足满二叉树的条件下用公式 节点数= 2^深度-1进行计算

  • 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int countNodes(TreeNode* root) {
        if(root == NULL) return 0;
        TreeNode * left =root->left;
        TreeNode * right =root->right;
        int left_dep=0,right_dep=0;
        while(left){
            left =left->left;
            left_dep++;
        }
        while(right){
            right =right->right;
            right_dep++;
        }
        if(left_dep==right_dep){
            return (2<<left_dep)-1;                                         //满二叉树公式法
        }
        return countNodes(root->left)+countNodes(root->right)+1;            //常规递归计算法
    }
};
赏